해석학 시리즈 목차
해석학 시리즈 1. 실수의 완비성, 상계와 하계, 상한과 하한 1-1. 아르키메데스 원리와 유리수의 조밀성의 증명 1-2. 단조 수렴 정리의 증명 2. 거리 공간 3. 열린 공, 근방, 내부점, 경계점 4. 집적
dimenchoi.tistory.com
칸토어의 축소구간 정리는 실수의 완비성으로부터 얻어지는 무수히 많은 정리 중 하나입니다.
엄청 대단해 보이는 이름과는 달리 정리 자체는 꽤나 직관적입니다.
칸토어의 축소구간 정리는 '집합을 끊임없이 수축할 수 있다' 정도로 요약할 수 있습니다.
이 문장의 엄밀한 수학적 설명이 무엇인지 지금부터 알아가 보겠습니다.
먼저 축소구간(Nested Interval)의 정의를 짚고 넘어가겠습니다.
축소구간의 정의.
$I_n = [a_n, b_n] \; (a_n \leq b_n)$이고 $I_{n+1} \subset I_n$일 때, $\lbrace I_n \rbrace$를 축소구간이라고 한다.
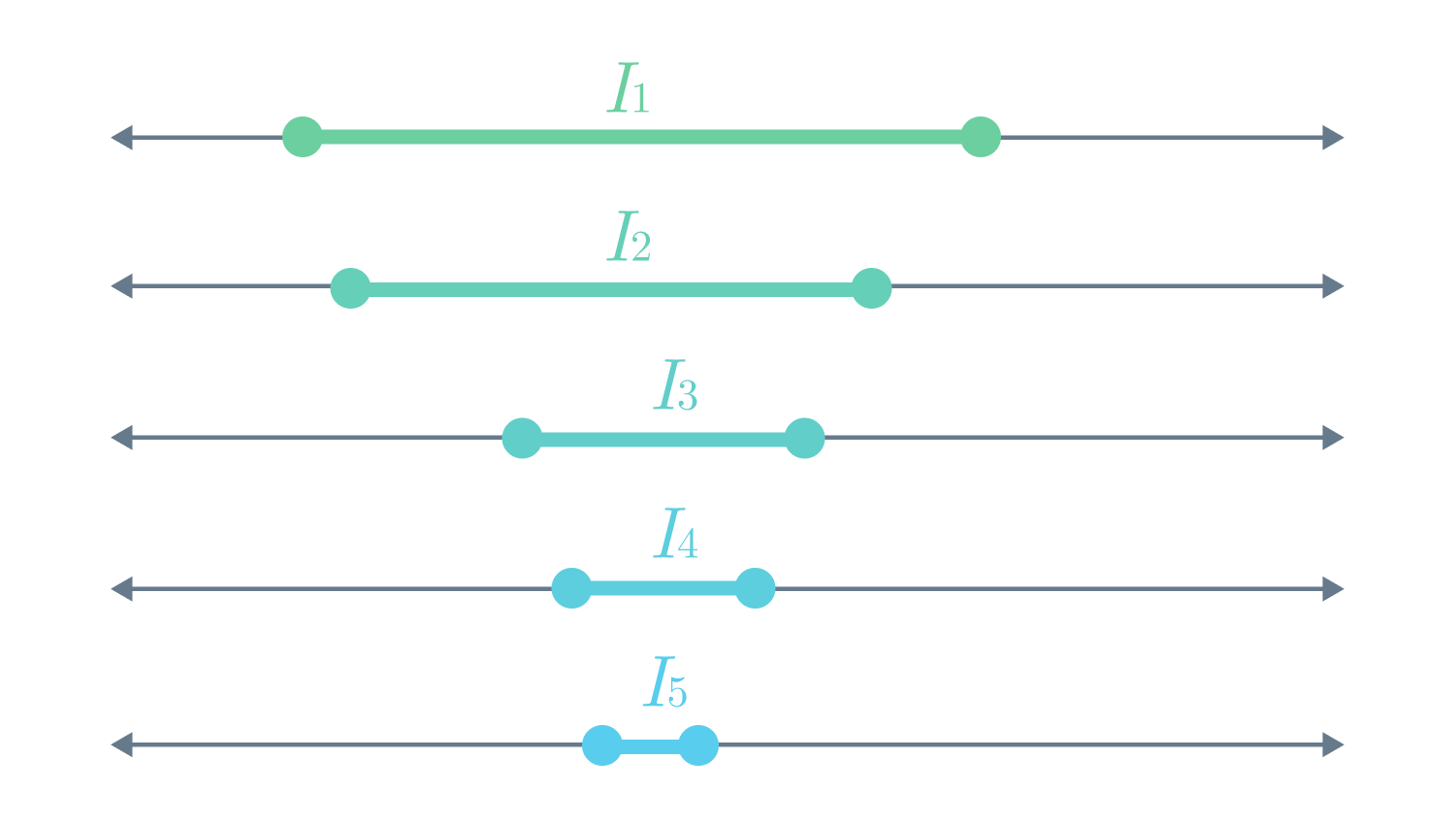
그런데 고등 수학 용어가 으레 그렇듯이, 축소구간의 번역은 책마다 조금씩 차이가 있습니다.
Nested Interval을 그대로 번역하여 내포된 구간이라는 표현을 사용하는 사람들도 있습니다.
그런데 '내포'라는 표현은 잘 안 와닿기 때문에 이 블로그에서는 축소구간이라는 표현을 사용하겠습니다.
칸토어의 축소구간 정리
축소구간 $[a_n, b_n]$에 대해 $\bigcap [a_n, b_n] \neq \emptyset$ 이며,
특히 $|b_n - a_n | \rightarrow 0$라면 홑원소 집합이다.
축소구간의 정의를 떠올리면 $\bigcap [a_n, b_n]$은
$\lbrace I_n \rbrace$이 유한할 경우, $\lbrace I_n \rbrace$의 마지막 구간과 같습니다.
하지만 $\lbrace I_n \rbrace$가 무한할 수도 있기 때문에,
칸토어의 축소구간 정리는 보다 일반적인 상황을 커버하기 위해 $\bigcap [a_n, b_n]$을 사용합니다.
이 정리의 증명은 실수의 완비성을 어디에서 사용해야 할지만 떠오른다면 간단합니다.
증명.
축소구간의 정의에 의해 모든 $n$에 대해 $a_1 \leq a_n \leq b_n \leq b_1$이 성립합니다.
따라서 $\lbrace a_n \rbrace$과 $\lbrace b_n \rbrace$은 유계인 수열입니다.
실수의 완비성에 의해 $\lbrace a_n \rbrace$는 상한 $\alpha$를, $\lbrace b_n \rbrace$는 하한 $\beta$를 가집니다.
이 때 모든 $n$에 대해 $a_n \leq \alpha \leq \beta \leq b_n$이 성립하므로(1), $\bigcap [a_n, b_n] = [\alpha, \beta] \neq \emptyset$입니다(2).
특히, $\lbrace a_n \rbrace$, $\lbrace b_n \rbrace$는 단조수열이므로,
단조수렴정리에 의해 $a_n \rightarrow \alpha$, $b_n \rightarrow \beta$입니다.
참고로 두 수열의 수렴값이 상한 및 하한과 같다는 사실은 단조수렴정리의 증명 과정을 보면 알 수 있습니다.
따라서 $|b_n - a_n| \rightarrow 0$은 $\alpha = \beta$를 의미하며, 이 때 $\bigcap [a_n, b_n] = [\alpha, \beta] = \lbrace \alpha \rbrace$는 홑원소 집합입니다. ◾️
이렇게 칸토어의 축소구간 정리의 증명을 알아봤습니다.
그런데 위 증명에는 두 가지 빠진 디테일이 있습니다.
(1) 모든 $n$에 대해 $a_n \leq b_n$이 성립한다면 $\sup a_n \leq \inf b_n$임을 보여야 합니다.
(2) $\bigcap [a_n, b_n] \subset [\alpha, \beta]$일 뿐만 아니라, $\bigcap [a_n, b_n] = [\alpha, \beta]$임을 보여야 합니다.
위 두 성질은 상한과 하한의 정의를 잘 사용하면 보일 수 있으며,
독자 분들이 도전해 볼 수 있는 문제로 남겨두겠습니다.
칸토어의 축소구간 정리는 볼차노 - 바이어슈트라스 정리라는 강력한 정리를 증명하는 데 필요합니다.
볼차노 - 바이어슈트라스 정리가 무엇인지에 대해서는 집적점의 개념을 배운 뒤 알아보도록 하겠습니다.
해석학 시리즈 목차
해석학 시리즈 1. 실수의 완비성, 상계와 하계, 상한과 하한 1-1. 아르키메데스 원리와 유리수의 조밀성의 증명 1-2. 단조 수렴 정리의 증명 2. 거리 공간 3. 열린 공, 근방, 내부점, 경계점 4. 집적
dimenchoi.tistory.com

'수학 > 해석학' 카테고리의 다른 글
| 집적점과 고립점 (Limit point and Isolation point) (2) | 2021.04.28 |
|---|---|
| 해석학 시리즈 목차 (0) | 2021.04.28 |
| 해석학의 중요한 기초 정리들 (0) | 2020.06.14 |
| 단조 수렴 정리의 증명 (0) | 2020.06.01 |
| 아르키메데스 원리와 유리수의 조밀성의 증명 (4) | 2020.06.01 |




