안녕하세요, Dimen입니다! 오늘부터 정수론에 대한 글을 써보고자 합니다. 정수론은 정규 수학 교육과정에서 잘 다루지 않기 때문에 많은 분들에게 생소한 분야입니다. 그런 만큼 많은 분들에게 도움이 될 것 같기 때문에 한 번 써보겠습니다.
정수론이란?
정수론은 말 그래도 정수를 다르는 학문입니다. 구체적으로 다른 수(유리수, 실수, 복소수)들은 가지지 않는, 정수의 독특한 특징인 약수와 배수, 몫과 나머지에 대해 탐구하는 학문입니다. 물론 고등정수론에서는 훨씬 더 깊은 정수론(여러분도 들어보셨을법한 리만 가설도 정수론의 영역입니다)도 다루지만, 이 시리즈에서는 기초정수론만 다루겠습니다.
그러면 정수론은 왜 필요할까요? 사실 19세기까지만 해도 정수론은 좋게 말해 순수학문, 나쁘게 말해 쓸모없는 학문으로 생각됐습니다. 그런데 컴퓨터의 발달 이후 정수론의 유용성은 급상승했습니다. 현재 정수론의 가장 큰 쓰임은 암호학일 것입니다. 현대 암호는 두 개의 무진장 큰 소수를 곱하는 것은 쉽지만, 이 결과를 다시 소인수분해하는 것은 어렵다는 원리를 기반으로 합니다. 구체적인 원리는 정수론의 몇 가지 정리를 알아야 이해할 수 있기 때문에, 시리즈의 맨 마지막에서 다시 얘기해 보겠습니다. 이외에도 컴퓨터를 이용한 계산이나 메모리 설계 등에서 정수론은 다양하게 쓰이고 있고, 아마 지금 이 글을 보고 계신 많은 분들도 이 쪽으로 필요해서 보고 있을 것이라 생각됩니다.
최대공약수와 최소공배수
정수론의 첫 번째 내용은 최대공약수(GCD, Greateast Common Division)와 최소공배수(LCM, Least Common Multiple)입니다. 두 개념의 정의와 구하는 방법은 중학교 때 다 배우셨을 겁니다. 먼저 두 수를 소인수분해를 한 뒤, 두 수의 공통된 소인수를 모두 곱하면 최대공약수, 두 수의 모든 소인수를 곱하면 최소공배수가 되죠. 간단하게 벤-다이어그램으로 정리하면 아래와 같습니다.
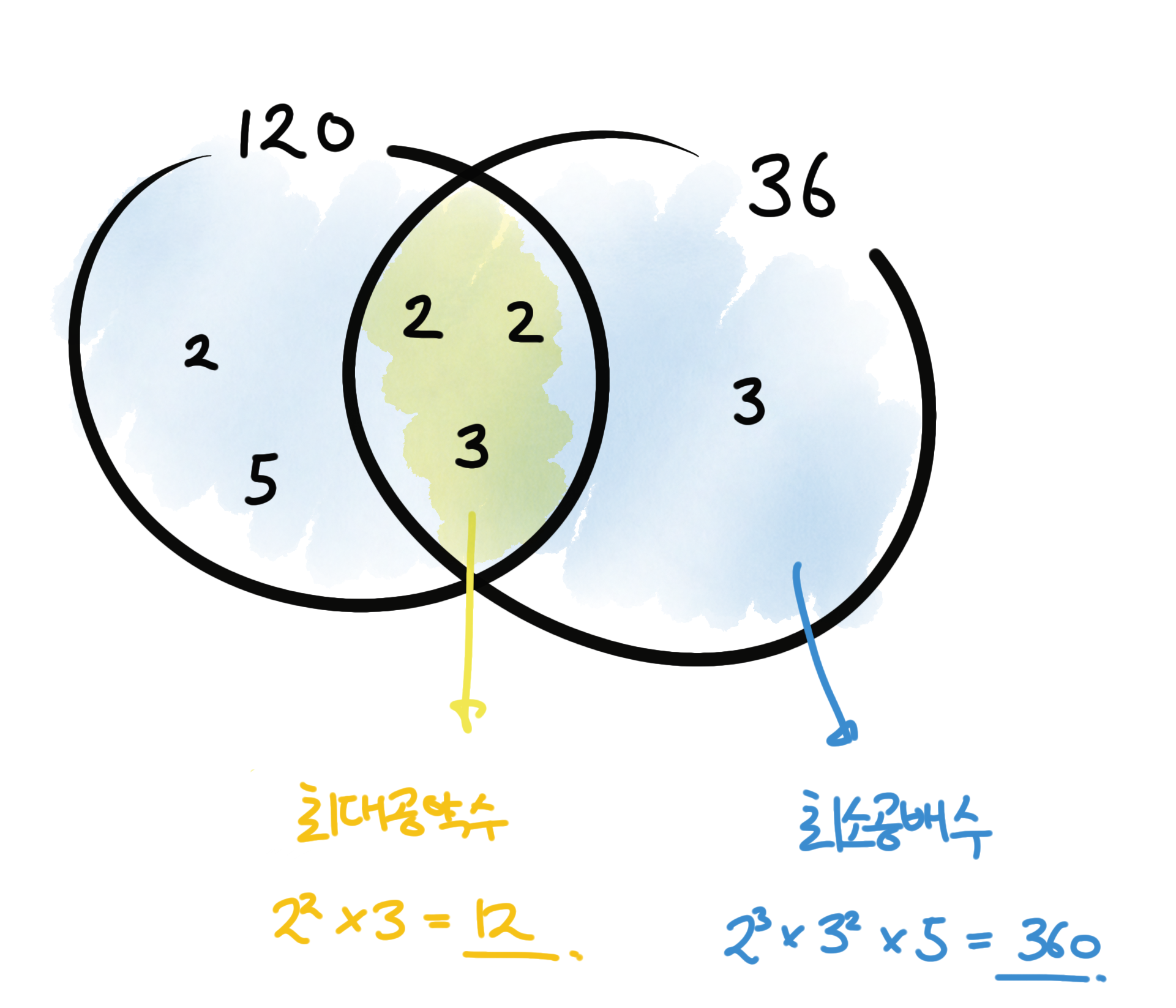
벤-다이어그램으로 최대공약수와 최소공배수를 표현하는 것은 여러가지 정리를 유도하는 데 큰 도움이 됩니다. 예를 들어서 두 수 $A, B$의 최대공약수를 $G$, 최소공배수를 $L$이라고 하면, 다음 식이 성립합니다.
$$
AB=LG
$$
이유는 벤-다이어그램에서 찾을 수 있습니다. $A$와 $B$를 곱하면 왼쪽의 초승달 부분과 오른쪽 초승달 부분은 한 번 곱해지고, 교집합 영역은 두 번 곱해집니다. 한편 $L$과 $G$를 곱해도 왼쪽의 초승달 부분과 오른쪽 초승달 부분은 한 번 곱해지고, 교집합 영역은 두 번 곱해집니다. 따라서 두 값이 같음을 알 수 있습니다.
정수론에서 두 수 $a, b$의 최대공약수와 최소공배수는 각각 $\text{gcd}(a, b), \text{lcm}(a, b)$으로 표기합니다.
유클리드 호제법
최대공약수를 찾을 때, 작은 수의 경우에는 사람이 직접 계산해서 찾을 수 있지만, 수가 무진장 커진다면 컴퓨터를 써야 합니다. 그런데 컴퓨터를 이용해 최대공약수를 찾을 때는, 위와 같이 소인수분해를 하기 보다는 유클리드 호제법이라는 알고리즘(문제를 풀기 위해 정해진 절차)를 사용하는 것이 더 빠릅니다. 유클리드 호제법은 다음 정리로부터 기인합니다.
$A$를 $B$로 나눈 몫을 $Q$라 하고, 나머지를 $R$이라 하자. 이 때, $\text{gcd}(A, B) = \text{gcd}(B, R)$이다.
예시를 보겠습니다. 60를 24로 나눈 몫은 2이고 나머지는 12입니다. 즉, $60=24\times 2 + 12$입니다. 과연 $\text{gcd}(60, 24) = \text{gcd}(24, 12)=12$임을 확인할 수 있습니다. 이 정리를 이용한 유클리드 호제법 알고리즘은 다음과 같습니다.
- $A$와 $B$의 최대공약수를 구하기 위해서 $A$를 $B$로 나눈 나머지 $R_1$을 구합니다.
- $B$를 $R_1$으로 나눈 나머지 $R_2$를 구합니다.
- $R_1$을 $R_2$로 나눈 나머지 $R_3$를 구합니다.
- 이 과정을 계속 반복하여, 어느 한 쪽이 나누어떨어질 때까지 반복합니다. 이 직전 얻은 나머지가 최대공약수입니다.
예를 들어 1254와 582의 최대공약수를 구해보겠습니다.
- $1254 = 582 \times 2 + 90$
- $582 = 90\times 6 + 42$
- $90 = 42 \times 2 + 6$
- $42 = 6 \times 7$
4단계에서 나누어떨어졌으며, 이 직전인 3단계의 나머지는 6이었습니다. 따라서 1254와 582의 최대공약수는 6입니다.
유클리드 호제법의 증명
유클리드 호제법은 귀류법을 사용해서 증명합니다. 즉, $\text{gcd}(A, B) \neq \text{gcd}(B, R)$를 가정하고 모순을 이끌겠습니다. 먼저 "$A$를 $B$로 나눈 몫을 $Q$라 하고, 나머지를 $R$이라 하자"라는 문장을 아래와 같이 수식으로 옮겨적겠습니다.
$$
A = BQ + R \quad (0\leq R<B)
$$
$\text{gcd}(A, B) = G$라 하겠습니다. $G$는 $A$와 $B$의 약수이므로, $A=aG, B=bG$로 쓸 수 있습니다. 여기서 $a, b$는 서로소입니다. 만약 $a, b$가 공약수를 가질 경우, $G$는 최대공약수가 아니기 때문입니다. 이 점이 나중에 중요하게 쓰입니다.
$A=aG, B=bG$을 위의 식에 대입하면 아래와 같습니다.
$$
aG = bGQ + R
$$
그런데 좌변이 $G$의 배수이므로, 우변도 $G$의 배수여야하며, 따라서 $R$도 $G$의 배수가 됨을 알 수 있습니다. 따라서 $R = rG$로 쓰고, 양변을 $G$로 나누면 아래와 같은 식을 얻습니다.
$$
a = bQ + r \quad (0\leq r<b)
$$
우변의 부등식은 $0 \leq R = rG< B=bG$에서 유도된 것입니다. 언뜻 보면 첫번째 식과 형태가 똑같지만, 이 식에서는 두 가지 중요한 조건이 추가됐습니다. 먼저, $a, b$가 서로소입니다. 또한 $b, r$은 서로소가 아닙니다. 만약 서로소였다면 이는 $B, R$의 최대공약수가 $G$임을 의미하는데, 이는 우리의 가정 $\text{gcd}(A, B) \neq \text{gcd}(B, R)$에 어긋나기 때문입니다.
이제 모순을 이끌겠습니다. $b, r$이 서로소가 아니므로 1이 아닌 공약수를 가지며, 이 공약수를 $g$라고 하겠습니다. 즉, $b = \beta g, r = \rho g$로 쓰겠습니다. 위 식에 대입하면 아래와 같습니다.
$$
a = \beta gQ + \rho g = g(\beta Q + \rho)
$$
그런데 이로부터 $a$ 역시 $g$의 배수가 됩니다. 즉, $a, b$는 공약수 $g$를 가지는데 이는 $a, b$가 서로소라는 사실에 모순됩니다. 이 모순은 우리의 가정, $\text{gcd}(A, B) \neq \text{gcd}(B, R)$이 틀렸기 때문입니다. 따라서 $\text{gcd}(A, B) = \text{gcd}(B, R)$입니다.
유클리드 호제법의 쓰임
유클리드 호제법은 최대공약수를 단순하면서도 빠르게 구할 수 있는 좋은 알고리즘입니다. 손으로 계산하기에는 그 차이를 못 느낄 수도 있지만 컴퓨터는 소인수분해보다 유클리드 호제법을 훨씬 더 빠르게 계산합니다. 컴퓨터적인 측면 이외에도 유클리드 호제법은 나중에 정수론의 여러 정리를 증명하는데 큰 도움이 됩니다. 정수론 얘기는 다음 글에서 덧셈 순환과 곱셈 순환에서 이어나가도록 하겠습니다.

'수학 > 정수론' 카테고리의 다른 글
| 정수론 (6) - 오일러의 정리와 오일러 파이 함수 (9) | 2020.01.23 |
|---|---|
| 정수론 (5) - 페르마의 소정리 (6) | 2020.01.19 |
| 정수론 (4) - 합동식에서의 나눗셈 (4) | 2020.01.17 |
| 정수론 (3) - 합동식 (6) | 2020.01.13 |
| 정수론 (2) - 베주 항등식 (7) | 2020.01.11 |




